179. –3; 0; 5 sonlaridan qaysilari tengsizliklar sistemasining yechimlari bo`ladi:
1
)
2) 
180. –2; 0; 1 sonlaridan qaysilari tengsizliklar sistemasining yechimlari bo`ladi:
1)
2) 
181. Tengsizliklar sistemaning yechimi bo`la oladigan barcha butun sonlarni toping
1)
2) 
3) 
4) 
182.
Berilgan qo`sh tengsizlikni qanoatlanturuvchi
sonlar
to`plamini sonli oraliqning belgilanishlari yordamida yozing va uni son o`qida
tasvirlang:
1) 1 ≤ x ≤ 5; 2) –1 ≤ x ≤ 3; 3) –1 < x < 4;
4) 1 < x < 2; 5) –3 ≤ x < 1; 6) –4 < x ≤ –2.
183. Berilgan son oraliqqa tegishli x sonlar to`plamini qo`sh tengsizlik ko`rinishida yozing va uni son o`qida tasvirlang:
1) [–4; 0]; 2) [–3; –1]; 3) (–4; –2);
4) (0; 3); 5) (–1; 4]; 6) [–2; 2).
184. 35- rasmda tasvirlangan x sonlar to`plamini qo`sh tengsizlik ko`rinishida, shuningdek, sonli oraliqning belgilanishlari yordamida yozing:
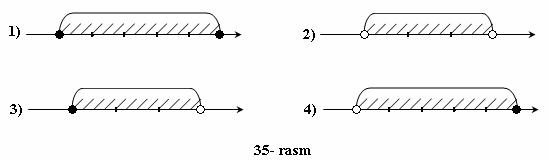
185. [2; 3] kesma (1; 4) oraliqqa tegishlimi?
186. [2; 4] va [3; 5] kesmalar umumiy nuqtalarga egami?
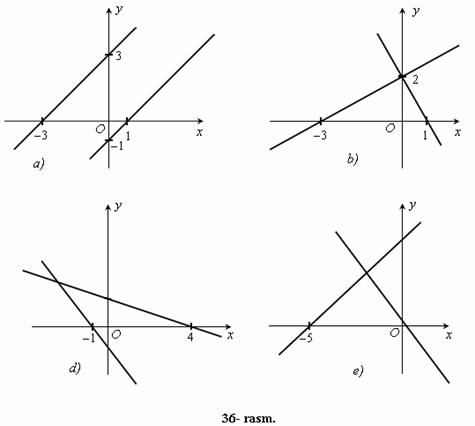
187. Bir koordinata tekisligida ikkita chiziqli funksiyaning grafiklari tasvirlangan (36- rasm). x ning qanday qiymatlarida ikki funksiyaning qiymati bir vaqtda musbat bo`ladi? Qanday qiymatlarida esa manfiy bo`ladi?
188.
Bir
koordinata tekisligida
y
= –2x – 2
va
funksiyalarning
grafiklarini yasang. Abssissalar o`qida
x
ning ikkala funksiyaning qiymatlari: 1) musbat; 2) manfiy bo`ladigan qiymatlari
to`plamini belgilang.
|
|
№ 2 TO`G`RI TO`RTBURCHAKNING TOMONLARI NATURAL SONLAR BILAN IFODA QILINADI. TO`G`RI TO`RTBURCHAK PERIMETRINING QIYMATI UNING YUZINING QIYMATIGA TENG BO`LISHI UCHUN ULAR QANDAY UZUNLIKLARGA EGA BO`LISHI KERAK? |
189. Tengsizlikni yeching:
1) (x – 3)(2x – 3) + 6x2 ≥ 2(2x – 3)2;
2) (5 – 6x)(1 + 3x) + (1 + 3x)2 ≤ (1 + 3x)(1 – 3x);
3) (2x + 1)(4x2 – 2x + 1) – 8x3 ≥ –2(x + 3);
4) (x – 2)(x2 + 2x + 4) ≤ x(x2 + 2) +1.
