Siz VI-VII sinf matematika kursida ratsional sonlar va ular ustida amallar bilan tanishgansiz. Ratsional son musbat son, manfiy son yoki nol soni bo`lishi mumkin.

Musbat ratsional son- bu  ko`rinishidagi sondir, bunda k va n- natural sonlar. Masalan, - musbat ratsional sonlar.

Manfiy ratsional son - bu  ko`rinishidagi sondir, bunda k va n – natural sonlar. Masalan,   - manfiy ratsional sonlar. Manfiy ratsional sonni  ko`rinishida yozish mumkin. Masalan,

 

Ratsional sonlar deb ko`rinishidagi sonlarga aytiladi, bunda m- butun son, n-natural son.

 

Agar ratsionla sonni maxraji 10 sonining natural darajasidan iborat kasr shaklida yozish mumkin bo`lsa, u holda bunday ratsional sonni o`nli kasr ko`rinishida tasvirlash qulay. Masalan,

 

 

Musbat sonlar noldan katta, manfiy sonlar esa noldan kichik deyiladi. Sonning noldan katta yoki kichikligini qisqacha yozish uchun >(katta) va <(kichik) tengsizlik ishoralaridan foydalaniladi. Jumladan, a>0 yozuvi a sonning noldan kattaligini, ya`ni a musbat son ekanini anglatadi; b<0 yozuvi b sonning noldan kichikligini, ya`ni b manfiy son ekanini anglatadi. Masalan:

 

 

> va < tengsizlik ishoralari qarama-qarshi ishoralar deyiladi. Masalan, 5>0 va 7>0 –bir xil ishorali tengsizliklar, 3>0 va -2<0 – qarama-qarshi ishorali tengsizliklar.

Sonlarning quyidagi xossalaridan mashqlar bajarishda ko`p foydalaniladi.

 

Harflar yordamida ifodalanishi

So`zlar yordamida ifodalanishi

1

2

1. Agar a>0 va b>0 bo`lsa, u holda a+b>0, ab>0,  bo`ladi.

Ikkita musbat sonning yig`indisi, ko`paytmasi va bo`linmasi musbat bo`ladi.

2. Agar a<0 va b<0 bo`lsa, u holda a+b<0, ab>0,  bo`ladi.

Manfiy sonlarning yig`indisi manfiy son, ikkita manfiy sonning ko`paytmasi va bo`linmasi esa musbat sonlar bo`ladi.

3. Agar a>0 va b<0 bo`lsa, u holda  ab<0, ,  bo`ladi.

Musbat son bilan manfiy sonning ko`paytmasi va bo`linmasi manfiy sonlar bo`ladi.

4. Agar ab>0 bo`lsa, u holda yoki a>0 va b>0, yoki a<0 va b<0 bo`ladi. Agar  bo`lsa, u holda yoki  a>0 va b>0, yoki a<0 va b<0 bo`ladi.

Agar ikkita sonning ko`paytmasi yoki bo`linmasi musbat bo`lsa, u holda bu sonlar bir xil ishoraga ega bo`ladi (ya`ni ikkala son musbat yoki ikkalasi manfiy bo`ladi).

5. Agar ab<0 bo`lsa, u holda yoki a>0 va b<0, yoki a<0 va b>0 bo`ladi. Agar  bo`lsa, u holda yoki  a>0 va b<0, yoki a<0 va b>0 bo`ladi.

Agar ikkita sonning ko`paytmasi yoki bo`linmasi manfiy bo`lsa, u holda bu sonlar har xil ishoraga ega bo`ladi (ya’ni ulardan biri musbat, ikkinchisi esa manfiy bo`ladi).

6. Agar ab=0 bo`lsa, u holda yoki a=0 va b≠0, yoki a≠0 va b=0, yoki a=0 va b=0 bo`ladi.

Agar ikkita sonning ko`paytmasi nolga teng bo`lsa, u holda shu sonlardan aqalli bittasi nolga teng bo`ladi.

7. Agar  bo`lsa, u holda a=0 va b≠0 bo`ladi.

Agar kasr nolga teng bo`lsa, u holda uning surati nolga teng bo`ladi, maxraji esa nolga teng bo`lmaydi.

 

Son o`qida musbat sonlar 0 nuqtadan o`ngda yotuvchi nuqtalar bilan, manfiy sonlar esa 0 nuqtadan chapda yotuvchi nuqtalar bilan tasvirlanishini bilasiz (22-rasm).

 

 

 

 

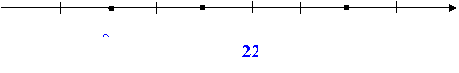
“a sonni tasvirlovchi nuqta” deyish o`rniga qisqalik uchun “a nuqta” deb aytiladi. Masalan, 3 nuqta 0 nuqtadan o`ngda yotadi; -2 nuqta 0 nuqtadan chapda yotadi (22-rasm).

1-m a s a l a. Agar a<0 bo`lsa, u holda a2>0 va a3<0 bo`lishini isbotlang.

Masalaning shartiga ko`ra a<0. Sonning kvadrati a2qa•a va ikkita manfiy sonning ko`paytmasi esa musbat son bo`lgani uchun a2>0.

Darajaning xossasiga ko`ra a2qa2•a, ya`ni a3 son a2 musbat son bilan a manfiy sonning ko`paytmasi bo`lgani uchun a3<0.

 

Manfiy sonni juft darajaga ko`targanda musbat son hosil bo`ladi. Manfiy sonni toq darajaga ko`targanda manfiy son hosil bo`ladi.

 

*Masalan, (-2,8)6>0, (-1,2)5<0.

 

*2-m a s a l a. Tenglamani yeching:

 

(2x+1)(3x-9)=0.

 

* Agar ko`paytuvchilardan aqalli bittasi nolga teng, ya`ni 2x+1=0 yoki 3x-9=0 bo`lsa, u holda ko`paytmani nolga teng bo`ladi. 2x+1=0 tenglamani yechib,  ekanini topamiz; 3x-9=0 tenglamani yechib, x=3 ekanini topamiz.

J a v o b:  

 

*3-m a s a l a. Tenglamani yeching:

 

 

* Berilgan kasr surati x2+5x=0 va maxraji x2+25≠0 bo`lganda nolga teng bo`ladi.

x2+5x=0 tenglamani bunday yozish mumkin:

 

x(x+5)=0.

 

Bu tenglama x1=0, x2=-5 ildizlarga ega. x=0 va x=-5 bo`lganda maxraj nolga teng emas: x2+25≠0.

J a v o b. x1=0, x2= -5.  

 

*4-m a s a l a. Tenglamani yeching:

 

*Agar x2-25=0, lekin x+5≠0 bo`lsa, u holda berilgan kasr nolga teng bo`ladi.

x2-25=0 tenglamani quyidagi ko`rinishda yozish mumkin:

 

(x-5)(x+5)=0,

bundan: x1=5, x2=-5. x=5 bo`lganda maxraj nolga teng emas: x+5≠0; x=-5 bo`lganda esa maxraj nolga teng: x+5=0. Demak, x=-5 berilgan tenglamaning ildizi bo`la olmaydi.

 

J a v o b. x=5.