1. T e n g s i z l i k l a r s i s t e m a l a r i .
M a s a l a
. Sig`imi
4000 l
bo`lgan bo`sh hovuz suv bilan to`ldirila boshlandi. Hovuzning
4
soatdan keyin yarmidan ko`prog`i to`lishi va
5
soatdan keyin u batamom to`lib-toshib ketmasligi uchun hovuzga soatiga necha
litrdan suv quyish kerak?
x
litr –
hovuzga 1
soat ichida quyiladigan suv miqdori bo`lsin. Masala shartiga ko`ra
4x > 2000, 5x ≤ 4000.
Birinchi tengsizlikdan x > 500, ikkinchi tengsizlikdan esa x ≤ 800 kelib chiqadi.
J a v o b .
Hovuzga soatiga
500 l
dan ko`p, lekin
800 l
dan ko`p bo`lmagan hajmda suv quyish kerak. 
4x > 2000 va 5x ≤ 4000 tengsizliklardagi noma;lum son ayni bir xil x sonidir. Shuning uchun bu tengsizliklar birgalikda qaraladi va tengsizliklar sistemasini tashkil qiladi, deyiladi:
(1)
Katta qavs x ning (1) sistemaning ikkala tengsizligini ham to`g`ri sonli tengsizlikka aylantiruvchi qismlarini topish kerakligini bildiradi.
(1) sistema bir noma’lumli chiziqli tengsizliklar sistemasiga misoldir.
Yana chiziqli tengsizliklar sistemasiga keltiriladigan bir noma’lumli tengsizliklar sistemalariga misoolar keltiramiz:
|
|
Bir noma’lumli tengsizliklar sistemasining yechimi deb, noma’lumning sistema tengsizliklarining barchasini to`g`ri sonli tengsizlikka aylantiruvchi qiymatiga aytiladi. Tengsizliklar sistemasini yechish – uning barcha yechimlarini topish yoki ularning yo`qligini aniqlash demakdir. |
Masalan,
x
= 1
ushbu
(2)
sistemaning yechimi bo`ladi, chunki x = 1 bo`lganda (2) sistemaning ikkala tengsizligi ham to`g`ri bo`ladi:
(2) sistemaning birinchi tengsizliginingikkala qismini 2 ga, ikkinchi tengsizligining ikkala qismini 3 ga bo`lib,
ni hosil qilamiz. Demak, (2) sistemaning yechimlari x ning –2 dan kichik bo`lmagan va 3 dan katta bo`lmagan barcha qiymatlaridan iborat bo`ladi.
x ≥ –2 va x ≤ 3 tengsizliklarni qo`sh tengsizlik ko`rinishida yozish mumkin:
–2 ≤ x ≤ 3.
S o n l i o r a l i q l a r . Bir noma’lumli tengsizliklar sistemalarining yechimlari har xil sonli top`lamlar bo`ladi. Bu to`plamlar o`zlarining nomlariga ega.
Masalan,
son o`qida
x
ning –2 ≤
x ≤ 3
bo`ladigan son qiymatlari to`plami oxirlari
–2
va 3
nuqtalarda bo`lgan kesma bilan tasvirlanadi (32- rasm).
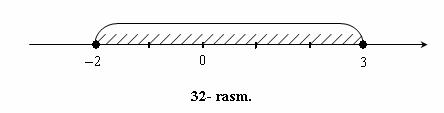
Shuning uchun –2 ≤ x ≤ 3 tengsizlikni qanoatlantiruvchi x sonlar to`plami kesma deb ataladi va [–2, 3] kabi belgilanadi.
|
|
Agar a < b bo`lsa, u holda a ≤ x ≤ b tengsizlikni qanoatlantiruvchi x sonlar to`plami kesma deyiladi va [a; b] kabi belgilanadi. |
Masalan,
[4; 7]
kesma – ushbu
4
≤ x ≤ 7
tengsizlikni qanoatlantiruvchi sonlar to`plami.
2 < x < 7, –1 ≤ x < 2, 4 < x ≤ 7 ko`rinishdagi tengsizliklarni qanoatlantiruvchi sonlar to`plami uchun ham alohida atamalar kiritiladi.
|
|
Agar a < b bo`lsa, u holda a < x < b tengsizlikni qanoatlantiruvchi x sonlar to`plami intervaldeyiladi va (a; b) kabi belgilanadi. |
Masalan,
(–2;
3)
interval – ushbu
–2 < x < 3
tengsizlikni qanoatlantiruvchi x sonlar to`plami (33- rasm).
|
|
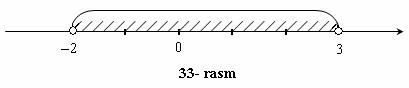
a ≤ x < b yoki a < x ≤ b tengsizlikni qanoatlantiruvchi x sonlar to`plami yarim intervallar deyiladi va mos ravishda [a; b) va (a; b] kabi belgilanadi. |
Masalan,
[–1;
2) yarim
interval – ushbu
–1 ≤ x < 2
tengsizlikni qanoatlantiruvchi
x
sonlar to`plami;
(4; 7]
yarim interval – ushbu
4 < x ≤ 7
tengsizlikni qanoatlantiruvchi
x
sonlar to`plami (34- rasm).
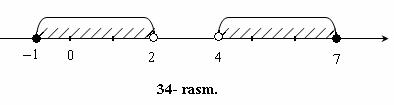
Kesmalar, intervallar, yarim intervallar va nurlar sonli oraliqlar deyiladi.
Shunday qilib, sonli oraliqlarni tengsizliklar ko`rinishida berish mumkin.
