Tengsizliklar sistemalarini yechishga doir misollar qaraymiz.

 1- m a s a l a .  Tengsizliklar sistemasini yeching:

                                                       (1)

  Birinchi tengsizlikni yechamiz:

5x – 1 > 3x + 3,

2x > 4,  x > 2.

Shunday qilib, birinchi tengsizlik x > 2 bo`lganda bajariladi.

Ikkinchi tengsizlikni yechamiz:

2x + 8 > x + 5,  x > –3.

Shunday qilib, (1) sistemaning ikkinchi tengsizligi x > –3 bo`lganda bajariladi.

Son o`qida (1) sistemaning birinchi va ikkinchi tengsizliklarining yechimlari to`plamini tsvirlaymiz.

Birinchi tengsizlikning yechimlari x > 2 nurning barcha nuqtalari, ikkinchi tengsizlikning yechimlari x > –3 nurning barcha nuqtalari bo`ladi (37- rasm).

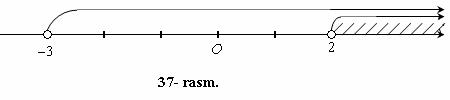
(1) sistemaning yechimlari x ning ikkala nurga bir vaqtda tegishli bo`lgan qiymatlari bo`ladi. Rasmdan ko`rinib turibdiki, bu nurlarning barcha umumiy nuqtalari to`plami x > 2 nur bo`ladi.

J a v o b .  x > 2.

2- m a s a l a .  Tengsizliklar sistemasini yeching:

                                                 (2)

  Birinchi tengsizlikni yeching:

3x – 3 ≤ 2x + 4,

x ≤ 7.

(2) sistemaning ikkinchi tengsizligini yechamiz:

4x ≥ 16, x ≥ 4.

Son o`qida (2) sistemaning birinchi va ikkinchi tengsizliklarining yechimlari to`plamini tasvirlaymiz. Birinchi tengsizlikning yechimlari x ≥ 7 nur, ikkinchi tengsizlikning yechimlari      x ≤ 4 nur bo`ladi (38- rasm).

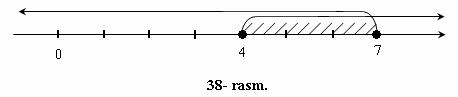
Rasmdan ko`rinib turibdiki, bu nurlarning umumiy nuqtalari to`plami [4; 7] kesma bo`ladi.

J a v o b .  4 ≤ x ≤ 7.

 3- m a s a l a .  Tengsizliklar sistemasini yeching:

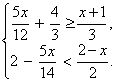                                                         (3)

 (3) sistemaning birinchi tengsizligini yechamiz:

5x + 16 ≥ 4x + 4,

x ≥ –12.

Ikkinchi tengsizlikni yechamiz:

28 – 5x < 14 – 7x,

2x < –14, x < –7.

Son o`qida x ≥ –12 va x < –7 nurlarni tasvirlaymiz (39- rasm). Rasmdan ko`rinib turibdiki, bu nurlarning umumiy nuqtalari to`plami [–12; –7) yarim interval iborat.

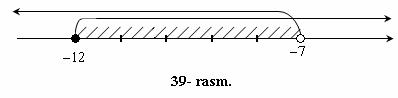
J a v o b .  –12 ≤ x < –7.

 4- m a s a l a .  Ushbu

                                                    (4)

tengsizliklar sistemaning yechimga ega emasligini ko`rsating.

 Birinchi tengsizlikni yechamiz:

2 – 2x < 4 – 3x,   x < 2.

(4) sistemaning ikkinchi tengsizligini yechamiz:

–3x < –9,

x > 3.

Son o`qida x < 2 va x > 3 nurlarni tasvirlaymiz (40- rasm).

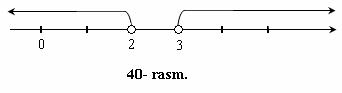
Rasmdan ko`rinib turibdiki, bu nurlar umumiy nuqtalarga ega emas.

Demak, (4) sistema yechimga ega emas.