

1. S o n n i n g m o d u l i .
Sonning moduli tushunchasini eslatib o`tamiz:
1) Musbat sonning moduli shu sonning o`ziga teng.
![]() Masalan,
|3|
= 3,
Masalan,
|3|
= 3, ![]() |2,4|
= 2,4.
|2,4|
= 2,4.
2) Manfiy sonning moduli unga qarama-qarshi songa teng,.
![]() Masalan,
|2|
= (2) = 2,
Masalan,
|2|
= (2) = 2, ![]() |1,5|
= (1,5) = 1,5.
|1,5|
= (1,5) = 1,5.
3) Nolning moduli nolga teng. |0| = 0.
Shunday qilib, son modulining tarifi quyidagicha bo`ladi:
|a| = a, agar a ≥ 0 bo`lsa,
|a| = a, agar a = 0 bolsa.
Bu tarif formula yordamida qisqacha bunday yoziladi:
|
|
|
Son modulining geometrik manosini qaraymiz.
Son o`qida, masalan, 3 va 2 nuqtalarni tasvirlaymiz (41- rasm). Rasmdan ko`rinib turibdiki, |3| = 3 bu 0 nuqtadan 3 nuqtagacha bo`lgan masofa, |2| = 2 bu 0 nuqtadan 2 nuqtagacha bo`lgan masofa.

Shunday qilib, |a| geometrik nuqtayi nazardan 0 nuqtadan a sonni tasvirlavchi nuqtagacha bo`lgan masofadir.
2. N o m a l u m m o d u l b e l g i s i o s t i d a q a t n a s h g a n t e n g l a m a l a r.
![]() 1-
m a s a l a . Tenglamani yeching:
1-
m a s a l a . Tenglamani yeching:
|x| = 7.
![]() 1)
x
≥ 0 bo`lsin. U
holda modulning tarifiga ko`ra
|x| = x
va tenglama bunday ko`rinishni oladi:
1)
x
≥ 0 bo`lsin. U
holda modulning tarifiga ko`ra
|x| = x
va tenglama bunday ko`rinishni oladi:
x = 7,
yani x = 7 berilgan tenglamaning ildizi;
2) x < 0 bo`lsin. U holda modulning tarifiga ko`ra |x| = x va tenglama bunday ko`rinishni oladi:
x = 7,
yani x = 7 berilgan tenglamaning ildizi.
J a v o b .
x1
= 7, x2 = 7. ![]()
![]() 2- m
a s a l a .
|3x + 2| = 1
tenglamani yeching.
2- m
a s a l a .
|3x + 2| = 1
tenglamani yeching.
![]() 1)
3x + 2
≥ 0 bo`lsin. Bu
holda 3x
+ 2 = 1, 3x = 1,
1)
3x + 2
≥ 0 bo`lsin. Bu
holda 3x
+ 2 = 1, 3x = 1, ![]() ;
;
2) 3x + 2 < 0 bo`lsin. Bu holda 3x + 2 = 1, 3x = 3, x = 1.
J a v o b .
![]() ,
x2 = 1.
,
x2 = 1. ![]()
3) N o m a l u m m o d u l b e l g i s i o s t i d a q a t n a s h g a n t e n g s i z l i k l a r .
Ushbu
|x| ≤ a, bunda a > 0,
tengsizlikni qaraymiz.
Bu tengsizlikni 0 nuqtadan a dan katta bo`lmagan masofada yotuvchi barcha x nuqtalar, yani [a, a] kesmaning nuqtalari qanoatlantiradi (42- rasm).
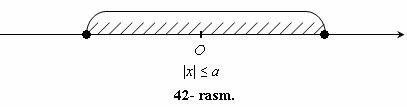
[a, a] kesma ushbu a ≤ x ≤ a tengsizlikni qanoatlantiruvchi x sonlar to`plami.
|
|
Demak, |x| ≥ a tengsizlik a ≤ x ≤ a qo`sh tengsizlikning ayni o`zini bildiradi, bunda a > 0. |
![]() Masalan,
|x|
= 2,5
tengsizlik
2,5 ≤ x ≤ 2,5
ni bildiradi;
|x| < 3
tengsizlik 3
< x < 3
ni bildiradi.
Masalan,
|x|
= 2,5
tengsizlik
2,5 ≤ x ≤ 2,5
ni bildiradi;
|x| < 3
tengsizlik 3
< x < 3
ni bildiradi.
![]() 3- m
a s a l a .
|5 3x| < 8
tengsizlikni yeching.
3- m
a s a l a .
|5 3x| < 8
tengsizlikni yeching.
![]() Berilgan
tengsizlikni bunday ko`rinishda yozamiz:
Berilgan
tengsizlikni bunday ko`rinishda yozamiz:
8 < 5 3x < 8.
Bu qo`sh tengsizlik quyidagi tengsizliklar sistemasining xuddi o`zini bildiradi:

![]()
Bu sistemani yechib,
![]() ekanini
topamiz (43- rasm).
ekanini
topamiz (43- rasm). ![]()
Ushbu
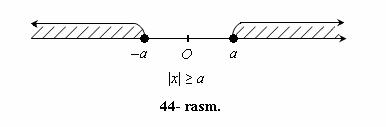
|x| ≥ a, bunda a > 0,
tengsizlikni qaraymiz.
Bu tengsizlikni 0 nuqtadan a dan kichik bo`lmagan masofada yotuvchi barcha x nuqtalar to`plami, yani x ≥ a va x ≤ a nurlarning nuqtalari qanoatlantiradi (44- rasm).
![]() 4- m
a s a l a . Tengsizlikni yeching:
|x 1| ≥ 2.
4- m
a s a l a . Tengsizlikni yeching:
|x 1| ≥ 2.
![]() 1)
x
1 ≥ 0 bo`lsin.
Bu holda x
1 ≥2.
quyidagi tengsizliklar sistemasini hosil qilamiz:
1)
x
1 ≥ 0 bo`lsin.
Bu holda x
1 ≥2.
quyidagi tengsizliklar sistemasini hosil qilamiz:
![]()
Bu sistemani yechib, x ≥ 3 ni topamiz.
2) x 1 < 0 bo`lsin. Bu holda (x 1) ≥ 2 yoki x 1 ≤ 2.
Quyidagi tengsizliklar sistemasini hosil qilamiz:
![]()
Bu sistemani yechib, x ≤ 1 ni topamiz.
Shunday qilib, |x 1| ≥ 2 tengsizlikning yechimlari birinchidan, x ≥ 3 sonlar, ikkinchidan, x ≤ 1 sonlar bo`ladi.
J a v o b .
x
≤ 1, x ≥ 3. ![]()
|x 1| ≥ 2 tengsizlikning yechimlari 45- rasmda tasvirlangan.

Agar
|x| ≤ a
tengsizlikda a son nolga teng bo`lsa, u holda tengsizlik x = 0 dan iborat birgina (yagona) yechimga ega bo`ladi, bordi-yu , agar a < 0 bo`lsa, u holda tengsizlik yechimga ega bo`lmaydi.
Agar
|x| ≥ a
tengsizlikda a son noldan kichik yoki unga teng bo`lsa, u holda u holda istalgan son uning yechimi bo`ladi.