1. R a t s i o n a l   s o n l a r .

Matematikada yangi sonlarning paydo bo`lishi u yoki bu amallarning bajarilishi zarurati tufayli sodir bo`ladi.

Natural sonlarni qo`shish va ko`paytirishda har doim natural son hosil bo`ladi. Ammo natural sondan natural sonni ayirishda hamma vaqt ham natural son hosil bo`lavermaydi.  Masalan, 2 – 5 ayirma natural son emas. Ayirish amalini hamma vaqt ham bajarish mumkin bo`lishi uchun manfiy butun sonlar va nol kiritilgan.

Natural sonlar to`plami butun sonlar to`plamigacha kengaytiriladi

…, −3, −2, −1, 0,1, 2, 3, … .

Butun sonlarni qo`shish, ayirish va ko`paytirishda har doim butun son hosil bo`ladi. Ammo butun sonni butun songa bo`lganda hamma vaqt ham butun son hosil bo`lavermaydi.  Masalan, 2 : 5 bo`’linma – butun son emas. Bo`lish amali hamma vaqt ham bajarilishi mumkin bo`lishi uchun ratsional sonlar, ya’ni  ko`rinishidagi sonlar kiritildi, bu yerda m – butun

son, n – natural son. Butun sonlar to`plami ratsional sonlar to`plamigacha kengaytirildi.

Ratsional sonni chekli yoki cheksiz o`nli kasr shaklida yozish mumkin.  Masalan,  va

  sozlarini chekli o`nli kasr shaklida yozish mumkin:   va  sonlarini

 burchak usulida bo`lishdan foydalanib, cheksiz o`nli kasr shaklida bunday yozish mumkin:

0,333… cheksiz o`nli kasr yozuvida 3 raqami takrorlanadi.

3 soni shu kasrning davri deyiladi; kasrning o`zi esa davrida 3 bo`lgan davriy kasr deyiladi, u 0,(3) ko`rinishida yoziladi va bunday o`qiladi: ”Nol butun davrda uch”.

0,454545… kasrning yozuvida 45 dan iborat ikkita raqam guruhi takrorlanadi; bu kasr davrida 45 bo`lgan davriy kasr deyiladi va u 0,(45) ko`rinishda yoziladi.

Yana cheksiz davriy kasrlarga misollar keltiramiz:

Istalgan ratsional sonni yoki chekli o`nli kasr, yoki o`nli davriykasr shaklida tasvirlash mumkin. Va aksincha, istalgan cheksiz davriy yoki chekli kasrni oddiy kasr shaklida, ya’ni

 shaklida tasvirlash mumkin, bu yerda m – butun son, n – natural son.

 1- m a s a l a .   sonini cheksiz o`nli kasr shaklida tasvirlang.

 “Burchak usuli”da bo`lish algoritmidan foydalanamiz:

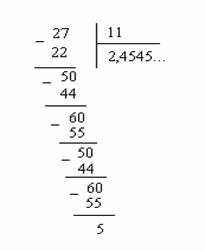
Qoldiqlar takrorlanayapti, shuning uchun bo`linmada aynan bir

raqamlar guruhi, ya’ni 45 takrorlanyapti. Demak, .

 2- m a s a l a .  Ushbu cheksiz o`nli davriy kasrni oddiy kasr shaklida tasvirlang: 1) 1,(7);  2) 0,2(18).

 1) x = 1,(7) = 1,777… bo`lsin, u holda 10x = 17,(7) = 17,777…

Ikkinchi tenglikdan birinchisini hadlab ayirib, 9x = 16 ni hosil qilamiz, bundan x = .

2) x = 0,2(18) = 0,2181818… bo`lsin, u holda

10x = 2,(181818) = 2,181818…,

1000x = 218,(18)= 218,181818… .

Uchinchi tenglikdan ikkinchisini hadlab ayirib, 990x = 216 ni hosil qilamiz, bundan

J a v o b .  1) 2)

2. I r r a t s i o n a l  s o n l a r .  H a q i q i y  s o n l a r .

Matematikada cheksiz o`nli davriy kasrlar bilan bir qatorda cheksiz

o`nli nodavriy kasrlar ham qaraladi.  Masalan:

0,1010010001…

kasrda birinchi 1 raqamidan keyin bitta nol, ikkinchi 1 raqamidan keyin ikkita nol, uchinchi 1 dan keyin uchta nol turibdi va hokazo, bu kasr nodavriy kasrdir. Shuningdek, verguldan keyin ketma-ket barcha natural sonlar yozilgan

0,123456…

kasr ham nodavriy kasrdir.

Cheksiz o`nli nodavriy kasrlar irratsional sonlar deyiladi. Ratsional va irratsional sonlar haqiqiy sonlar to`plamini tashkil qiladi.

Haqiqiy sonlar ustida arifmetik amallar va taqqoslash qoidalari shunday kiritiladiki, natijada bu amallarning, tenglik va tengsizliklarning ratsional sonlar uchun xossalari butunlay saqlanadi.

Kvadrat ildiz chiqarish amaliga murojaat qilamiz.

Oliy matematika kursida istalgan haqiqiy nomanfiy sondan kvadrat ildiz chiqarish mumkinligini isbot qilamiz.

 Masalan,− ratsional son, … − irratsional son.

 va hokazo sonlar, ya’ni natural sonlarning kvadratlari bo`lmagan natural sonlardan olingan kvadrat ildizlar ham irratsional sonlardir.

 Irratsional sonlar faqat kvadrat ildiz chiqarish natijasidagina hosil bo’lmasligini ta’kidlaymiz.  Masalan, aylana uzunligining uning diametriga nisbatiga teng bo’lgan  soni irratsional sondir.  sonini irratsional sondan kvadrat ildiz chiqarish yo’li bilan hosil qilib bo’lmaydi.

         Amalda kvadrat ildizlarning talab qilingan aniqlikdagi taqribiy qiymatlarini topish uchun jadvallar, mikrokalkulatorlar va boshqa hisoblash vositalaridan foydalaniladi.

         3 – m a s a l a.  ni  taqribiy hisoblash formulasi yordamida

hisoblang, bunda   va yaqinlashish xatoligi

 dan oshmaydi.

         Yaqinlashish xatoligi esa

         Demak, haqiqiy son 0,002 gacha aniqlikda 4,125 ratsional son

bilan almashtirilishi mumkin.     

Shunday qilib, irratsional sonlar ustida amallar amaliy jihatdan ularning o’nli yaqinlashishlari ustida amallar bilan almashtiriladi.

Geometrik nuqtai nazardan haqiqiy sonlar son o’qining nuqtalari bilan tasvirlanadi (46 - rasm).

Har bir haqiqiy songa son o’qining yagona nuqtasi mos keladi va son o’qining har bir nuqtasiga yagona haqiqiy son  mos keladi.