Agar  kvadrat tenglamada  yoki c koeffitsiyentlardan aqalli bittasi nolga teng bo’lsa, u holda bu tenglama chala kvadrat tenglama deyiladi.

Demak, chala kvadrat tenglama quyidagi tenglamalardan biri ko’rinishida bo’ladi:

,                                                     (1)

,                                       (2)

,                                   (3)

 (1), (2), (3) tenglamalarda  koeffitsiyent nolga teng emasligini eslatib o’tamiz.

Chala kvadrat tenglamalar qanday yechilishini ko’rsatamiz.

 1 – m a s a l a. Tenglamani yeching:

 Bu tenglamaning ikkala qismini 5 ga bo’lib,

ni hosil qilamiz, bundan .  

 2 – m a s a l a. Tenglamani yeching:

 Tenglamaning ikkala qismini 3 ga bo’lamiz:

Bu tenglamani quyidagicha yozish mumkin:

,

bundan  

 3 – m a s a l a. Tenglamani yeching:

 Tenglamani bunday yozish mumkin:

.

Bu tenglamani haqiqiy ildizlarga ega emas, chunki  ning istalgan haqiqiy qiymatlarida  bo’ladi.

 4 – m a s a l a. Tenglamani yeching:

 Tenglamaning chap qismini ko’paytuvchilarga ajratib,

ekanini hosil qilamiz, bundan:  

Javob.  .
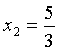