Bundan oldingi paragrafda kvadrat tenglamalarni to’la kvadratni ajratish usuli bilan yechish qaralgan edi. Shu usulni umumiy ko’rinishdagi kvadrat tenglamani yechish formulasini keltirib chiqarish uchun qo’llaymiz.

Umumiy ko’rinishdagi kvadrat tenglamani qaraymiz:

,

bunda .

Tenglamaning ikkala qismini  ga bo’lib,

kvadrat tenglamani hosil qilamiz.

Bu tenglamaning shaklini shunday almashtiramizki, uning chap qismida ikkihadning to’la kvadrati hosil bo’lsin:

,

,

.

Agar  bo’lsa, u holda

.

Bundan

,

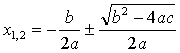
yoki        

(2) formula umumiy ko’rinishdagi kvadrat tenglama ildizlari formulasi deyiladi.

 1 – m a s a l a. Tenglamani yeching:

 Bu yerda . (2) formula bo’yicha quyidagilarni topamiz:

,

bundan

,       

Javob. ,    .

 2 – m a s a l a.   tenglamani yeching.

 Bu yerda . (2) formula bo’yicha quyidagilarni topamiz:

.

Javob. .

Agar (1) tenglikning o’ng qismida manfiy son tursa, ya’ni  bolsa, u holda (1) tenglik  ning hech qanday haqiqiy qiymatida to’g’ri bo’lmaydi, chunki uning chap qismi nomanfiy. Shuning uchun, agar  bo’lsa,

tenglama haqiqiy ildizlarga ega bo’lmaydi.

 3 – m a s a l a.  tenglama haqiqiy ildizlarga ega emasligini isbotlang.

 Bu yerda ,

Demak, berilgan tenglama haqiqiy ildizlarga ega emas.

 4 – m a s a l a.  tenglamani yeching:

 (2) formula bo’yicha quyidagiga ega bo’lamiz:

.

Ildiz belgisi ostida turgan son manfiy:

.

Javob. Tenglama haqiqiy ildizlarga  ega emas.

Haqiqiy ildizlarning yo’qligiga (2) formula yordamida ham ishonch hosil qilish mumkin.

Chala kvadrat tenglamalarni ham (2) formula bo’yicha yechish mumkin, biroq ularni yechishda 31 - § da qaralgan usullardan foydalanish qulayroq.