Bu tenglamada bosh koeffitsiyent birga teng.  Masalan,

tenglama keltirilgan kvadrat tenglamadir.

 Masalan,  tenglamani 4 ga bo’lib, quyidagi shaklga keltiriladi:

.

 (1) keltirilgan kvadrat tenglamaning ildizlarini topamiz. Buning uchun umumiy ko’rinishdagi  kvadrat tenglama ildizlari formulasidan, ya’ni

                                     (2)

formuladan foydalanamiz. Umumiy ko’rinishdagi tenglamada  ,     bo’lsa, keltirilgan kvadrat tenglama

hosil bo’ladi. Shu sababli keltirilgan kvadrat tenglam uchun (2) formula

Yoki

                            (3)

ko’rinishga ega bo’ladi.

(3) formula keltirilgan kvadrat tenglama ildizlari formulasi deyiladi.

(3)  formuladan, ayniqsa, p juft son bo’lganda foydalanish qulay.

 Masalan,  tenglamani yechaylik.

  (3) formula bo’yicha quyidagini topamiz:

Javob. , .

Keltirilgan kvadrat tenglama uchun quyidagi teorema o’rinli:

 (3) formula bo’yicha:

,

.

Bu tengliklarni hadlab qo’shsak,  bo’ladi. Bu tengliklarni ko’paytirib, kvadratlar ayirmasi formulasi bo’yicha quyidagini hosil qilamiz:

.

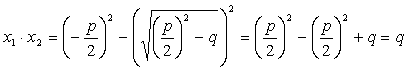 Masalan,  tenglama ,  ildizlarda ega; uning ildizlari yig’indisi , ularning ko’paytmasi esa .

Viyet teoremasi kvadrat tenglama ikkita teng  ildizlarga ega bo’lgan holda ham to’g’ri bo’lishini ta’kidlab o’tamiz.

 Masalan,  tenglama ikkita teng  ildizlarga ega; ularning yig’indisi , ko’paytmasi .

 1 – m a s a l a.  tenglamaning ildizlaridan biri . Shu tenglamaning p koeffitsiyentini va ikkinchi ildizi  ni toping.

Viyet teoremasiga ko’ra:

, 

 bo'lgani uchun , bundan ,

.

Javob. , .

 2 – m a s a l a. Ildizlari ,  bo’lgan keltirilgan kvadrat tenglama tuzing.

 ,  sonlari  tenglamaning ildizlari bo’lgani uchun Viyet teoremasiga ko’ra ,

Javob. .

  3 – m a s a l a.  tenglamaning ildizlaridan biri musbat. Tenglamani yechmasdan, ikkinchi ildizning ishorasini aniqlang.

 Tenglamaning ikkala qismini 3 ga bo’lib, quyidagini hosil qilamiz:

Viyet teoremasiga ko’ra . Shartga ko’ra , demak, .

Ba’zi masalalarni yechishda Viyet teoremasiga teskari bo’lgan quyidagi teorema qo’llaniladi.

 Chap qismidagi

ifodada  p ning o’rniga ni, q ning o’rniga esa  ko’paytmani qo’yamiz. Natijada quyidagi ifoda hosil bo’ladi:

Shunday qilib, agar p, q, ,  sonlar (4) munosabatlar bilan bog’langan bo’lsa, u holda  ning har qanday qiymatida

tenglik bajariladi, bundan esa  va  lar  tenglamaning ildizlari ekani kelib chiqadi.

Viyet teoremasiga teskari teoremadan foydalanib, kvadrat tenglamaning ildizlarini ba’zan tanlash usuli bilan topish mumkin.

 4 – m a s a l a. Tanlash usuli bilan

tenglamaning ildizlarini toping.

Bu yerda p=-5, q=6. Ikkita  va  sonni

,   

bo’ladigan qilib tanlaymiz.

          va  ekanini e’tiborga olib, Viyet teoremasiga teskari teorema bo’yicha ,  ga, ya’ni  tenglamaning ildizlariga ega bo’lamiz.

 5 – m a s a l a.   kasrni ixchamlang.

 Kasrning suratini ko’paytuvchilarga ajratamiz:

Demak,

.

 ko’phad kvadrat uchhad deyiladi, bunda .

5 – masalani yechishda  kvadrat uchhad guruhlash usuli bilan ko’paytuvchilarga ajratildi. Uni quyidagi teoremadan foydalanib ham ko’paytuvchilarga ajratish mumkin edi.

 (5) tenglikning o’ng qismida turgan ifodaning shaklini almashtiramiz:

      (6)

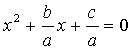          va lar  tenglamaning, ya’ni  tenglamaning ildizlari bo’lgani uchun Viyet teoremasiga ko’ra,

,   

bundan  , .

Bu ifodalarni (6) tenglikka qo’yib, (5) formulani hosil qilamiz.

 6 – m a s a l a.  ifodani soddalashtiring.

 Kasrning surat va maxrajini ko’paytuvchilarga ajratamiz.

1)  tenglama ikkita ildizga ega:

, .

Isbot qilingan teoremaga ko’ra

.

2)  tenglama ,  ildizlarga ega. Isbot qilingan teoremaga ko’ra

Shunday qilib,

.