1 – m a s a l a. Tenglamani yeching:

.

  deb belgilaymiz. Bu holda tenglama quyidagi ko’rinishni oladi:

.

Bu kvadrat tenglamani yechamiz:

,

 bo’lgani uchun berilgan tenglamani yechish quyidagi ikkita tenglamani yechishga keltiriladi:

,

bundan:

,

Javob. , .

          deb belgilash bilan bu tenglama kvadrat tenglamaga keltiriladi.

 2 – masala. Bikvadrat tenglamani yeching:

  deb belgilaymiz. Bu holda

Bu kvadrat tenglamani yechib, quyidagilarni topamiz:

,

 tenglama  ildizlarga ega,  tenglama esa haqiqiy ildizlarga ega emas.

Javob. .

 3 – m a s a l a. Tenglamani yeching:

 Tenglamadagi kasrlarning umumiy maxraji ga teng. Agar    va  bo’lsa, u holda tenglamaning ikkala qismini   ga ko’paytirib, quyidagini hosil qilamiz:

.

Bu tenglamaning shaklini almashtiramiz:

,

,

Hosil bo’lgan kvadrat tenglamani yechib, uning ildizlarini topamiz:

; 

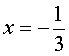 va  bo’lganda berilgan kasrlarning maxrajlari nolga aylanmaganligi uchun 1 va  sonlari shu tenglamaning  ildizlari bo’ladi.

Javob. ;  .

 4 – m a s a l a. Tenglamani yeching:

                       (1)

 Shartga ko’ra . Tenglamaning ikkala qismini

ga ko’paytirib, quyidagini hosil qilamiz:

.

Bu tenglamaning shaklini almashtiramiz:

,

                           (2)

Hosil bo’lgan kvadrat tenglamani yechib, uning ildizlarini topamiz:

,

 bo’lganda berilgan tenglamadagi maxrajlar nolga aylanmaydi. Demak, – 1 soni – berilgan tenglamaning ildizi.  bo’lganda berilgan tenglamadagi ikkita kasrning maxraji nolga teng. Shuning uchun 2 soni berilgan tenglamaning ildizi bo’lmaydi.

Javob. .

4 – masalada berilgan (1) tenglama ikkita ildizga ega bo’lgan (2) kvadrat tenglamaga keltirildi. Ulardan biri, ya’ni  (1) tenglamaning ildizi bo’ladi. Ikkinchi ildiz (1) tenglamaning ildizi bo’lmaydi. Bu holda u chet ildiz deyiladi.

Shunday qilib, tenglamani noma’lum ishtirok etgan ifodaga ko’paytirganda chet ildizlar paydo bo’lishi mumkin. Shuning uchun noma’lum kasr maxrajida qatnashgan tenglamalarni yechganda tekshirish o’tkazish zarur.

 5 – m a s a l a. Tenglamani yeching:

  kvadrat uchhadni ko’paytuvchilarga ajratamiz.  tenglamani yechib, uning ,  ildizlarini topamiz. Shuning uchun .

Tenglamaning ikkala qismini kasrlarning umumiy maxrajiga, ya’ni  ga ko’paytiramiz. Natijada quyidagiga ega bo’lamiz.

Bu tenglamaning shaklini almashtiramiz:

,

.

Bu tenglamani yechib, uning ildizlarini topamiz:

,

Bu ildizlarni tekshiramiz.  bo’lganda berilgan tenglama ikkinchi va uchinchi kasrlarining maxrajlari nolga aylanadi. Shuning uchun  - chet ildiz.  bo’lganda berilgan tenglama kasrlarining maxrajlari nolga teng emas. ni berilgan tenglamaga qo’yib, bu son tenglamaning ildizi bo’lishiga ishonch hosil qilish mumkin.

Javob. .