* 1- m a s a l a .  Tenglamalar sistemasini yeching:

                     (1)

 

* x va y shunday sonlarki, (1) ning ikkala tengligi ham to‘g‘ri, ya’ni x, y (1) sistemaning yechimi bo‘ladi, deb faraz qilamiz.

Bu tengliklarni hadlab qo‘shamiz. Bu holda yana to‘g‘ri tenglik hosil bo‘ladi, chunki teng sonlarga teng sonlar qo‘shilayapti:

 

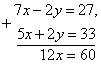
bundan 

Endi x=5 ni (1) sistema tenglamalarining biriga, masalan, birinchi tenglamasiga qo‘yamiz: 7·5–2y=27. Bu tenglikdan topamiz:

35–2y=27,  –2y=–8,  y=4.

Shunday qilib, agar (1) sistema yechimga ega bo‘lsa, u holda bu yechim faqat ushbu sonlar jufti bo‘lishi mumkin: x=5, y=4.

Endi x=5, y=4, haqiqatan ham, (1) sistemaning yechimi ekanligiga ishonch hosil qilish kerak. Buni oddiygina tekshirish bilan bajarish mumkin:

7·5–2·4=27,

5·5+2·5=33.

Ikkala tenglik ham to‘g‘ri tenglik.

Shunday qilib, (1) sistema birgina yechimga ega: x=5, y=4.

Tenglamalar sistemasini yechishning ko‘rib chiqilgan bu usuli algebraik qo‘shish usuli deyiladi. Noma’lumlardan birini yo‘qotish uchun sistema tenglamalarining chap va o‘ng qismlarini qo‘shish yoki ayirish kerak.

* 2- m a s a l a .  Tenglamalar sistemasini yeching: 

 

* Birinchi tenglamadan ikkinchisini hadlab ayiramiz:

 

bundan  

y=3 ni sistemaning birinchi tenglamasiga qo‘yamiz: 5x+3·3=29

Bu tenglamani yechib, topamiz: 5x+9=29,   5x=20,   x=4.

Javob: x=4, y=3.

Ko‘rib chiqilgan masalalardan ravshanki, sistemani yechishda algebraic qo‘shish usuli ikkala tenglamaning ham biror noma’lum oldidagi koeffitsiyentlari bir xil yoki faqat ishoralari bilan farq qilgan holda qulay bo‘ladi. Agar bunday bo‘lmasa, u holda sistemaning har bir tenglamasining chap va o‘ng qismlarini mos keladigan sonlarga ko‘paytirish yo‘li bilan biror noma’lum oldidagi koeffitsiyentlarning modullarini tenglashtirishga urinib ko‘rish kerak.

* 3- m a s a l a .  Tenglamalar sistemasini yeching:

 

* Agar sistemaning birinchi tenglamasining ikkala qismini 3 ga, ikkinchisini esa 2 ga ko‘paytirib, ikkinchi tenglamadan birinchisini hadlab ayirilsa, u holda birdaniga x ning qiymati topiladi:

                                 

                          

x=–6 qiymatni sistemaning birinchi tenglamasiga qo‘yib, topamiz: –18+2y=10, 2y=28,  y=14.

Javob:  x=–6,  y=14.

 

Shunday qilib, tenglamalar sistemasini algebraik qo‘shish usuli bilan yechish uchun:

1)    noma’lumlardan birining oldida turgan koeffitsiyentlar modullarini tenglashtirish;

2)    hosil qilingan tenglamalarni hadlab qo‘shib yoki ayirib, bitta noma’lumni topish;

3) topilgan qiymatni berilgan sistemaning tenglamalaridan biriga qo‘yib, ikkinchi noma’lumni topish kerak.

 

* 4- m a s a l a .  Tenglamalar sistemasini yeching:

 

* 1) Birinchi tenglamani o‘zgarishsiz qoldirib, ikkinchi tenglamani 4 ga ko‘paytiramiz:

 

2) (3) sistemaning ikkinchi tenglamasidan birinchi tenglamani hadlab ayirib, topamiz: 11y=–22, bundan y=–2.

3) y=–2 ni (2) sistemaning ikkinchi tenglamasiga qo‘yib, topamiz: x+2·(-2)=–2, bundan x=2.

Javob: x=2, y=–2.