Ushbu sistema berilgan bo‘lsin:

      (1)

Avval birinchi tenglamani qaraymiz:

x–y=–1.           (2)

Bu tenglamaning koordinata tekisligidagi geometric tasviri bo‘lib uning grafigi xizmat qiladi.

Ikki noma’lumli birinchi darajali

ax+by=c

 

tenglamaning grafigi deb, bu tenglamaga x va y koordinatalarini qo‘yganda uni to‘g‘ri tenglikka aylantiruvchi M (x; y) nuqtalar to‘plamiga aytiladi.

 

 (2) tenglamaning grafigini yasash uchun bu tenglamada y ni x orqali ifoda qilamiz:

y=x+1.            (3)

(2) va (3) tenglamalar x va y sonlar orasidagi bir xil bog‘lanishni ifoda qiladi: x va y sonlarning istagan jufti uchun yoki (2) va (3) tengliklar to‘g‘ri, yoki ikkala tenglik ham noto‘g‘ri bo‘ladi. Shuning uchun bu tenglamalarning grafigi bir xil. (3) funksiyaning grafigi to‘g‘ri chiziq bo‘lgani uchun shu to‘g‘ri chiziqning o‘zi (2) tenglamaning ham grafigi bo‘ladi.

To‘g‘ri chiziqni yasash uchun uning ikkita nuqtasini topish yetarli. Masalan, (2) tenglamadan topamiz: agar x=0 bo‘lsa, u holda y=1 bo‘ladi; agar x=–1 bo‘lsa, u holda y=0 bo‘ladi. Shunday qilib, (2) tenglamaning grafigi (0; 1) va (–1; 0) nuqtalardan o‘tuvchi to‘g‘ri chiziq bo‘ladi (17- rasm).

 


 

Xuddi shuningdek, birinchi darajali ikki noma’lumli ax+by=c ko‘rinishdagi istalgan tenglamaning grafigi, agar a yoki b sonlardan aqalli bittasi nolga teng bo‘lmasa, to‘g‘ri chiziq bo‘lishini ko‘rsatish mumkin.

 

 (1) sistema ikkinchi tenglamasi

2x+y=4             (4)

   ning grafigini yasaymiz (18- rasm).

Bu tenglamadan topamizki, agar x=0 bo‘lsa, u holda y=4 bo‘ladi, agar y=0 bo‘lsa, u holda x=2 bo‘ladi.

Demak, (4) tenglamaning grafigi (0; 4) va (2; 0) nuqtalardan o‘tuvchi to‘g‘ri chiziq bo‘ladi (18- rasm).

Yasalgan ikkala to‘g‘ri chiziqning kesishish nuqtasini qaraymiz. 19- rasmdan ko‘rinib turibdiki, uning koordinatalari (1; 2) bo‘ladi. Bu nuqta ikkala to‘g‘ri chiziqqa ham tegishli bo‘lgani uchun x=1 va y=2 bo‘lganda (2) va (4) tenglamalarning ikkalasi ham to‘g‘ri tenglikka aylanadi, ya’ni x=1 va y=2 (1) sistemaning yechimi bo‘ladi.

Tenglamalar sistemasini yechishning grafik usuli quyidagidan iborat:

1)  sistema har bir tenglamasining grafigi yasaladi;

2)  yasalgan to‘g‘ri chiziqlar kesishish nuqtasining (agar ular kesishsa) koordinatalari topiladi.

Tenglamalar grafiklari kesishish nuqtasining koordinatalari shu tenglamalar sistemasining yechimi bo‘ladi.

Grafik usul ko‘pgina amaliy masalalarning taqribiy yechimlarini topishda qo‘llaniladi.

Tenglamalar sistemasi nechta yechimga ega bo‘lishi mumkinligini grafiklar yordamida osongina aniqlash mumkin.

 

Tekislikda ikki to‘g‘ri chiziq – tenglamalar sistemasi grafiklarning o‘zaro joylashuvida uch hol bo‘lishi mumkin:

(1)            To‘g‘ri chiziqlar kesishadi, ya’ni bitta umumiy nuqtaga ega bo‘ladi. Bu holda tenglamalar sistemasi bitta (yagona) yechimga ega bo‘ladi ((1) sistema uchun 19- rasmga qarang).

(2)            To‘g‘ri chiziqlar parallel, ya’ni ular umumiy nuqtalarga ega emas. Bu holda tenglamalar sistemasi yechimlarga ega bo‘lmaydi.

(3)            To‘g‘ri chiziqlar ustma-ust tushadi. Bu holda sistema cheksiz ko‘p yechimlar to‘plamiga ega bo‘ladi.

 

 

Oxirgi ikki hol uchun misollar keltiramiz.

* 1-m a s a l a .  Ushbu

 

tenglamalar sistemasi yechimlarga ega emasligini ko‘rsating.

* (5) sistemaning birinchi tenglamasini 2 ga ko‘paytiramiz va hosil bo‘lgan tenglamadan berilgan sistemaning ikkinchi tenglamasini hadlab ayiramiz:

 

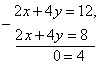
Noto‘g‘ri tenglik hosil bo‘ldi. Demak, x va y uning (5) sistemasining ikkala tengligi ham to‘g‘ri bo‘la oladigan qiymatlari yo‘q, ya’ni (5) sistema yechimlarga ega emas.

Bu geometrik nuqtai nazardan (5) sistema tenglamalarining grafiklari parallel to‘g‘ri chiziqlar bo‘lishini anglatadi (20- rasm).

* 2-m a s a l a . Ushbu

 

   tenglamalar sistemasi cheksiz ko‘p yechimlarga ega ekanligini ko‘rsating.

 

 (6) sistemaning birinchi tenglamasidan x ni y orqali ifoda qilamiz:

x=2+2y.

 

x ning bu qiymatini sistemaning ikkinchi tenglamasiga qo‘yib, hosil qilamiz:

3(2+2y)–6y=6,

6+6y–6y=6,

6=6.

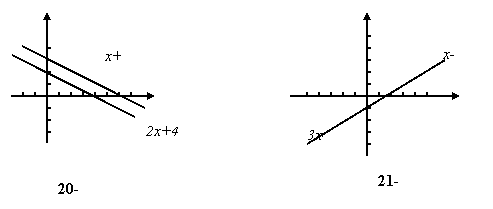
To‘g‘ri tenglik hosil bo‘ldi. Shunday qilib, y ning istagan qiymatida x=2+2y va y sonlar (6) sistemaning ikkala tenglamasini ham to‘g‘ri tenglikka aylantiradi, ya’ni (6) sistema cheksiz ko‘p yechimlar to‘plamiga ega bo‘ladi.

Bu geometrik nuqtai nazardan (6) sistema ikkala tenglamasining grafiklari ustma-ust tushishini bildiradi (21- rasm).